Analysis of movies- IMDB dataset

We will look at a subset sample of movies, taken from the Kaggle IMDB 5000 movie dataset
Inspecting the dataset
movies <- read_csv(here::here("data", "movies.csv"))
glimpse(movies)## Rows: 2,961
## Columns: 11
## $ title <chr> "Avatar", "Titanic", "Jurassic World", "The Aveng…
## $ genre <chr> "Action", "Drama", "Action", "Action", "Action", …
## $ director <chr> "James Cameron", "James Cameron", "Colin Trevorro…
## $ year <dbl> 2009, 1997, 2015, 2012, 2008, 1999, 1977, 2015, 2…
## $ duration <dbl> 178, 194, 124, 173, 152, 136, 125, 141, 164, 93, …
## $ gross <dbl> 7.61e+08, 6.59e+08, 6.52e+08, 6.23e+08, 5.33e+08,…
## $ budget <dbl> 2.37e+08, 2.00e+08, 1.50e+08, 2.20e+08, 1.85e+08,…
## $ cast_facebook_likes <dbl> 4834, 45223, 8458, 87697, 57802, 37723, 13485, 92…
## $ votes <dbl> 886204, 793059, 418214, 995415, 1676169, 534658, …
## $ reviews <dbl> 3777, 2843, 1934, 2425, 5312, 3917, 1752, 1752, 3…
## $ rating <dbl> 7.9, 7.7, 7.0, 8.1, 9.0, 6.5, 8.7, 7.5, 8.5, 7.2,…skim(movies)| Name | movies |
| Number of rows | 2961 |
| Number of columns | 11 |
| _______________________ | |
| Column type frequency: | |
| character | 3 |
| numeric | 8 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| title | 0 | 1 | 1 | 83 | 0 | 2907 | 0 |
| genre | 0 | 1 | 5 | 11 | 0 | 17 | 0 |
| director | 0 | 1 | 3 | 32 | 0 | 1366 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| year | 0 | 1 | 2.00e+03 | 9.95e+00 | 1920.0 | 2.00e+03 | 2.00e+03 | 2.01e+03 | 2.02e+03 | ▁▁▁▂▇ |
| duration | 0 | 1 | 1.10e+02 | 2.22e+01 | 37.0 | 9.50e+01 | 1.06e+02 | 1.19e+02 | 3.30e+02 | ▃▇▁▁▁ |
| gross | 0 | 1 | 5.81e+07 | 7.25e+07 | 703.0 | 1.23e+07 | 3.47e+07 | 7.56e+07 | 7.61e+08 | ▇▁▁▁▁ |
| budget | 0 | 1 | 4.06e+07 | 4.37e+07 | 218.0 | 1.10e+07 | 2.60e+07 | 5.50e+07 | 3.00e+08 | ▇▂▁▁▁ |
| cast_facebook_likes | 0 | 1 | 1.24e+04 | 2.05e+04 | 0.0 | 2.24e+03 | 4.60e+03 | 1.69e+04 | 6.57e+05 | ▇▁▁▁▁ |
| votes | 0 | 1 | 1.09e+05 | 1.58e+05 | 5.0 | 1.99e+04 | 5.57e+04 | 1.33e+05 | 1.69e+06 | ▇▁▁▁▁ |
| reviews | 0 | 1 | 5.03e+02 | 4.94e+02 | 2.0 | 1.99e+02 | 3.64e+02 | 6.31e+02 | 5.31e+03 | ▇▁▁▁▁ |
| rating | 0 | 1 | 6.39e+00 | 1.05e+00 | 1.6 | 5.80e+00 | 6.50e+00 | 7.10e+00 | 9.30e+00 | ▁▁▆▇▁ |
Besides the obvious variables of title, genre, director, year, and duration, the rest of the variables are as follows:
gross: The gross earnings in the US box office, not adjusted for inflationbudget: The movie’s budgetcast_facebook_likes: the number of facebook likes cast memebrs receivedvotes: the number of people who voted for (or rated) the movie in IMDBreviews: the number of reviews for that movierating: IMDB average rating
Are there any missing values (NAs)? Are all entries distinct or are there duplicate entries?
No missing but many duplicates across categories. There are 2961 rows and only 2907 unique movie titles, so it can be inferred that some movies show more than 1 times with different genres.
General Analysis
How many movies of each genre are in this dataset?
movies %>%
count(genre) %>%
arrange(desc(n))## # A tibble: 17 x 2
## genre n
## <chr> <int>
## 1 Comedy 848
## 2 Action 738
## 3 Drama 498
## 4 Adventure 288
## 5 Crime 202
## 6 Biography 135
## 7 Horror 131
## 8 Animation 35
## 9 Fantasy 28
## 10 Documentary 25
## 11 Mystery 16
## 12 Sci-Fi 7
## 13 Family 3
## 14 Musical 2
## 15 Romance 2
## 16 Western 2
## 17 Thriller 1Exploring the relationship between earnings and budget in each film genre
movies %>%
mutate(return = gross/budget) %>%
group_by (genre) %>%
summarise (average_earnings = mean(gross), average_budget = mean(budget), return_on_budget = mean(return)) %>%
arrange(desc(return_on_budget))## # A tibble: 17 x 4
## genre average_earnings average_budget return_on_budget
## <chr> <dbl> <dbl> <dbl>
## 1 Horror 37713738. 13504916. 88.3
## 2 Biography 45201805. 28543696. 22.3
## 3 Musical 92084000 3189500 18.8
## 4 Family 149160478. 14833333. 14.1
## 5 Documentary 17353973. 5887852. 8.70
## 6 Western 20821884 3465000 7.06
## 7 Fantasy 42408841. 17582143. 6.68
## 8 Animation 98433792. 61701429. 5.01
## 9 Comedy 42630552. 24446319. 3.71
## 10 Mystery 67533021. 39218750 3.27
## 11 Romance 31264848. 25107500 3.17
## 12 Drama 37465371. 26242933. 2.95
## 13 Adventure 95794257. 66290069. 2.41
## 14 Crime 37502397. 26596169. 2.17
## 15 Action 86583860. 71354888. 1.92
## 16 Sci-Fi 29788371. 27607143. 1.58
## 17 Thriller 2468 300000 0.00823Table of summary statistics for the 15 top grossing directors
movies %>%
group_by(director) %>%
summarise(total_amount = sum(gross),mean_amount = mean(gross), median_amount = median(gross), SD_amount = sd(gross, na.rm= TRUE)) %>%
slice_max(n=15, total_amount) ## # A tibble: 15 x 5
## director total_amount mean_amount median_amount SD_amount
## <chr> <dbl> <dbl> <dbl> <dbl>
## 1 Steven Spielberg 4014061704 174524422. 164435221 101421051.
## 2 Michael Bay 2231242537 171634041. 138396624 127161579.
## 3 Tim Burton 2071275480 129454718. 76519172 108726924.
## 4 Sam Raimi 2014600898 201460090. 234903076 162126632.
## 5 James Cameron 1909725910 318287652. 175562880. 309171337.
## 6 Christopher Nolan 1813227576 226653447 196667606. 187224133.
## 7 George Lucas 1741418480 348283696 380262555 146193880.
## 8 Robert Zemeckis 1619309108 124562239. 100853835 91300279.
## 9 Clint Eastwood 1378321100 72543216. 46700000 75487408.
## 10 Francis Lawrence 1358501971 271700394. 281666058 135437020.
## 11 Ron Howard 1335988092 111332341 101587923 81933761.
## 12 Gore Verbinski 1329600995 189942999. 123207194 154473822.
## 13 Andrew Adamson 1137446920 284361730 279680930. 120895765.
## 14 Shawn Levy 1129750988 102704635. 85463309 65484773.
## 15 Ridley Scott 1128857598 80632686. 47775715 68812285.How do movies across different genres perform on IMDB ratings?
movies %>%
group_by(genre) %>%
summarise(count=n(), mean_rating=mean(rating), min_rating=min(rating), max_rating=max(rating), median_rating=median(rating), SD_rating=sd(gross, na.rm= TRUE)) %>% arrange(desc(count))## # A tibble: 17 x 7
## genre count mean_rating min_rating max_rating median_rating SD_rating
## <chr> <int> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 Comedy 848 6.11 1.9 8.8 6.2 48067667.
## 2 Action 738 6.23 2.1 9 6.3 94846029.
## 3 Drama 498 6.73 2.1 8.8 6.8 51331049.
## 4 Adventure 288 6.51 2.3 8.6 6.6 96677829.
## 5 Crime 202 6.92 4.8 9.3 6.9 38309059.
## 6 Biography 135 7.11 4.5 8.9 7.2 49220303.
## 7 Horror 131 5.83 3.6 8.5 5.9 31505660.
## 8 Animation 35 6.65 4.5 8 6.9 86201928.
## 9 Fantasy 28 6.15 4.3 7.9 6.45 27036114.
## 10 Documentary 25 6.66 1.6 8.5 7.4 29441650.
## 11 Mystery 16 6.86 4.6 8.5 6.9 54787287.
## 12 Sci-Fi 7 6.66 5 8.2 6.4 30917838.
## 13 Family 3 6.5 5.7 7.9 5.9 247535241.
## 14 Musical 2 6.75 6.3 7.2 6.75 126255330.
## 15 Romance 2 6.65 6.2 7.1 6.65 44107152.
## 16 Western 2 5.70 4.1 7.3 5.70 29101851.
## 17 Thriller 1 4.8 4.8 4.8 4.8 NAggplot(movies, aes(x=rating))+
geom_density(aes(fill=genre), alpha = 0.3, show.legend = FALSE)+
facet_wrap(~genre, nrow = 6)+
labs(title="Ratings distributed by genre",
x ="ratings",
caption = "Source: IMDB dataset")+
theme_bw()+
NULL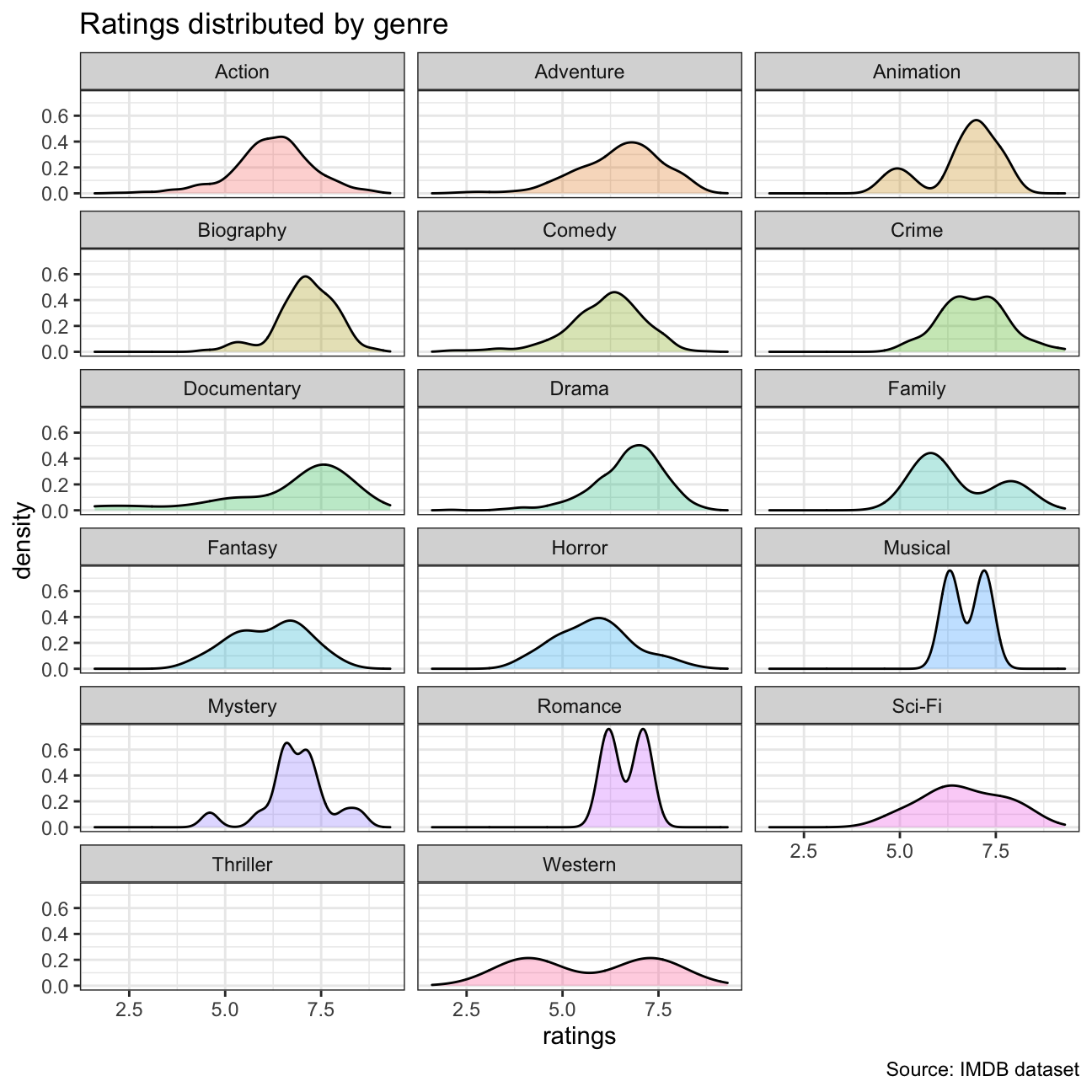
Are Facebook likes a good predictor of box office revenue of a movies?
The number of facebook likes that the cast has received is not a good predictor of how much money a movie will make at the box office since the correlation coefficient is only ~0.2, too low to indicate a correlation between these two. Since the Gross Revenue vs Facebook Likes plot is hard to read, we decided to map Log of the number of FB likes to the X axis and Log of gross revenue to the Y axis.
cor(movies$cast_facebook_likes, movies$gross)## [1] 0.213 ggplot(movies, aes(x=cast_facebook_likes, y= gross))+
geom_point()+
geom_smooth(method = "lm")+
theme_bw()+
NULL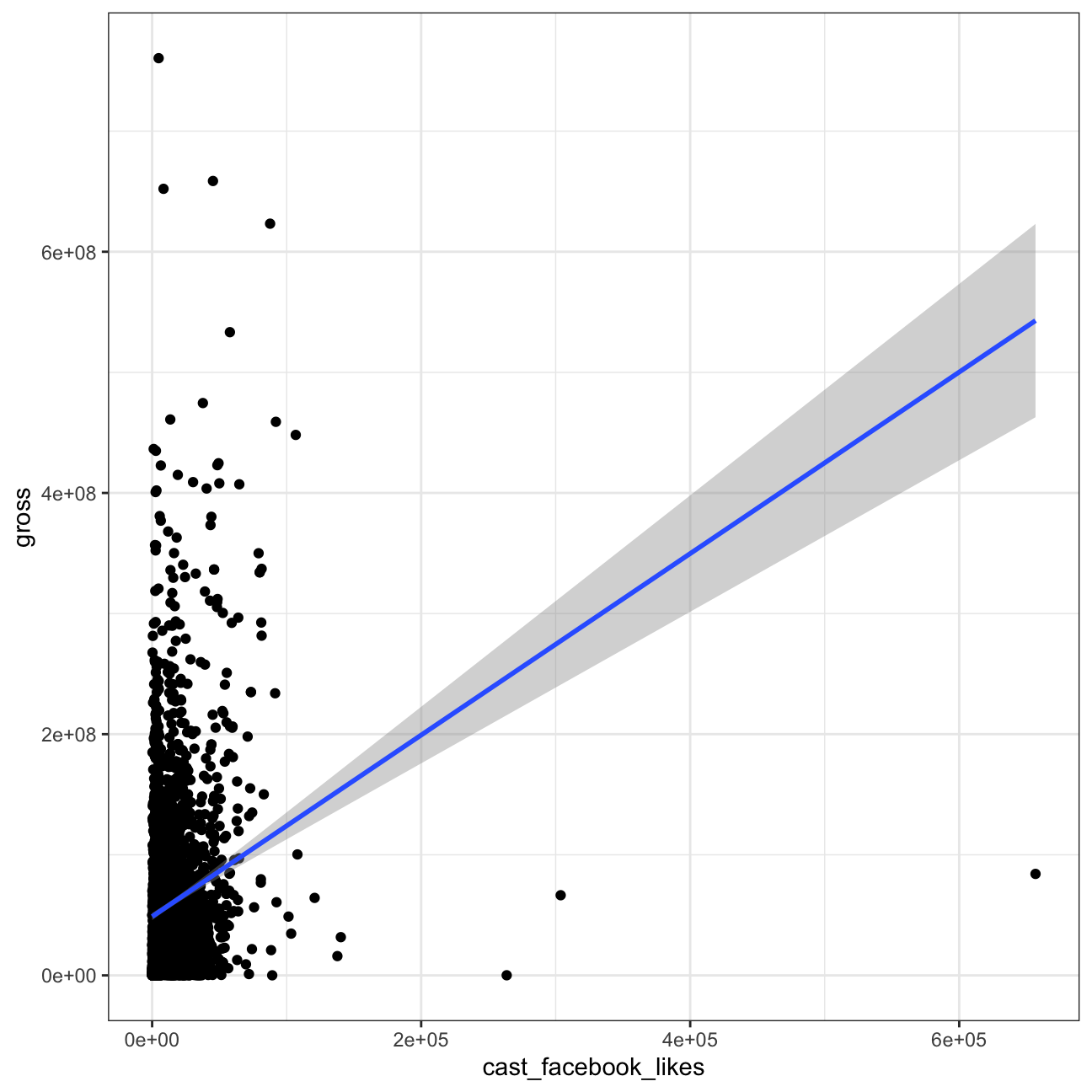
fblikes = movies %>%
select(gross, cast_facebook_likes) %>%
mutate(ln_gross=log(gross), ln_fblikes=log(cast_facebook_likes))
ggplot(fblikes, aes(x=ln_fblikes, y= ln_gross))+
geom_point()+
geom_smooth(method = "lm")+
theme_bw()+
labs(
x = "Log of the number of FB likes",
y= "Log of gross revenue" ,
title = "How do Facebook likes correlate to box office performance?",
caption = "Source: IMDB Dataset"
)+
NULL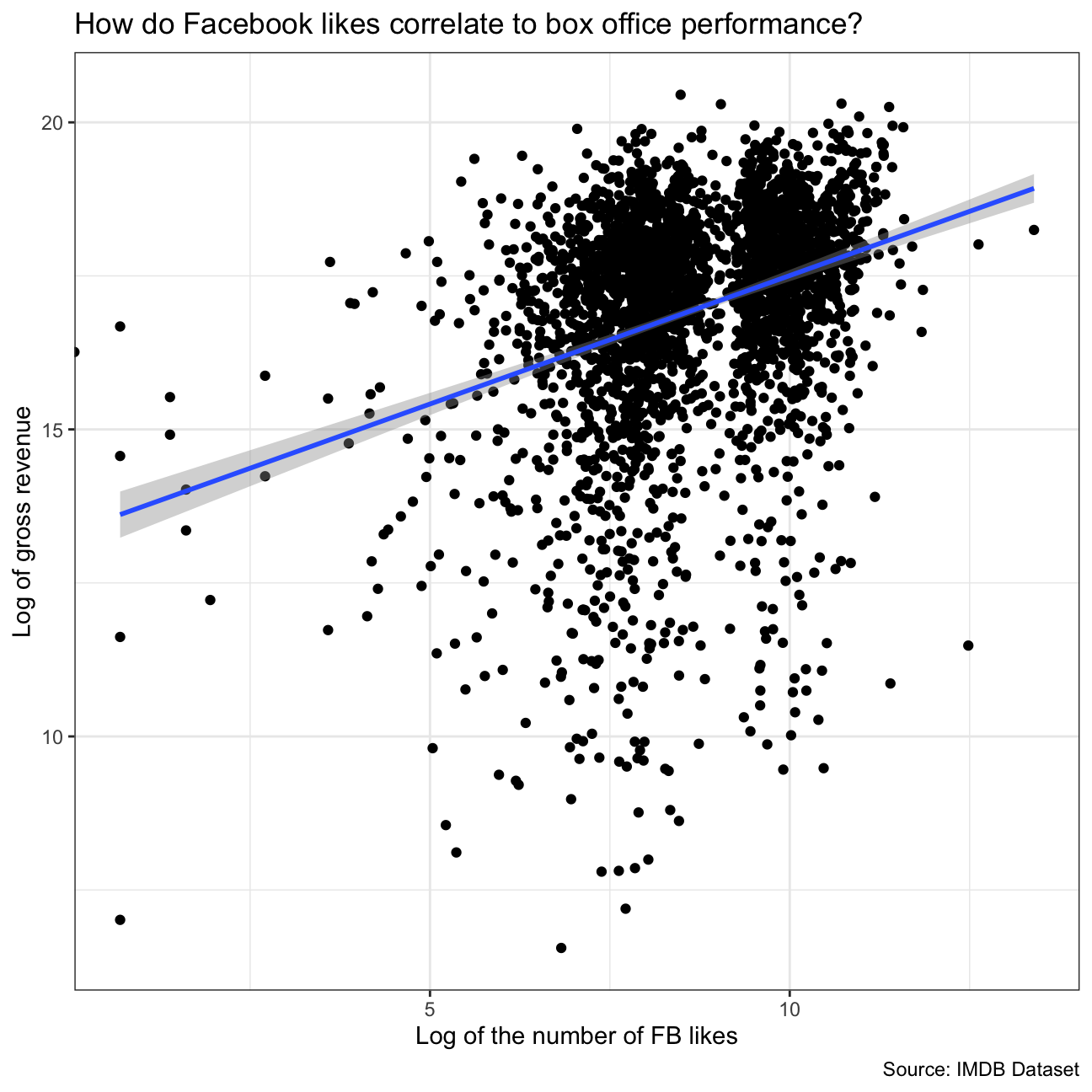
How does the budget size correlate with movie revenue performance?
The budget is likely to be a good predictor of how much money a movie will make at the box office since the correlation coefficient is about ~0.64, indicating a correlation between these two. Since the first Gross revenue vs budget graph is difficult to interpret we follow it up with another graph in which we decided to map the log of the budget size to the X axis and the log of gross revenue to the Y axis
cor(movies$budget, movies$gross)## [1] 0.641ggplot(movies, aes(x=budget, y= gross))+
geom_point()+
geom_smooth(method = "lm")+
theme_bw()+
NULL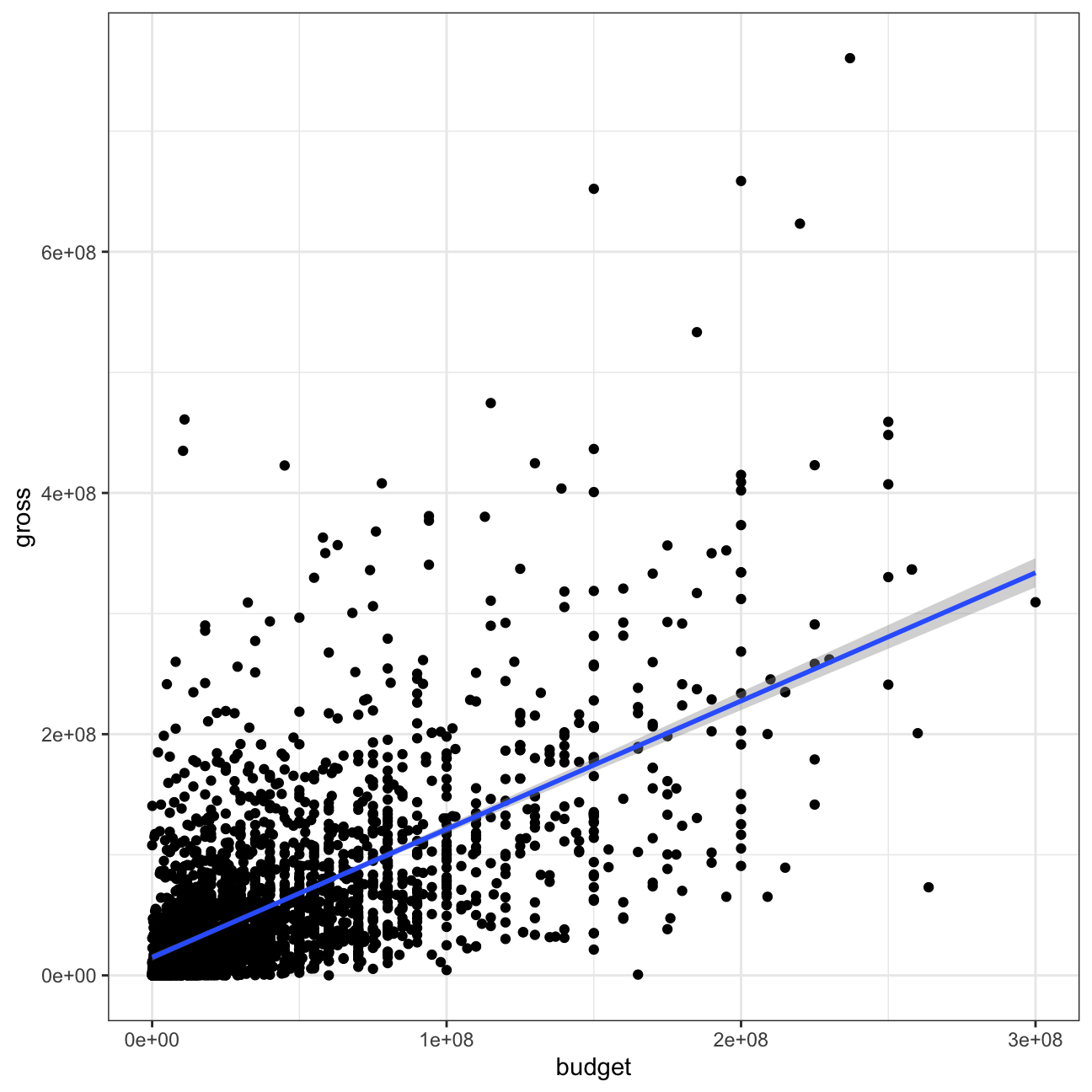
gross_on_budget = movies %>%
select(gross, budget) %>%
mutate(ln_gross=log(gross), ln_budget=log(budget))
ggplot(gross_on_budget, aes(x=ln_budget, y= ln_gross))+
geom_point()+
geom_smooth(method = "lm", fill="lightgrey")+
theme_bw()+
labs(
x = "Log of film budget",
y= "Log of gross revenue" ,
title = "Is a bigger budget a good predictor of box office success?",
caption = "Source: IMDB Dataset") +
NULL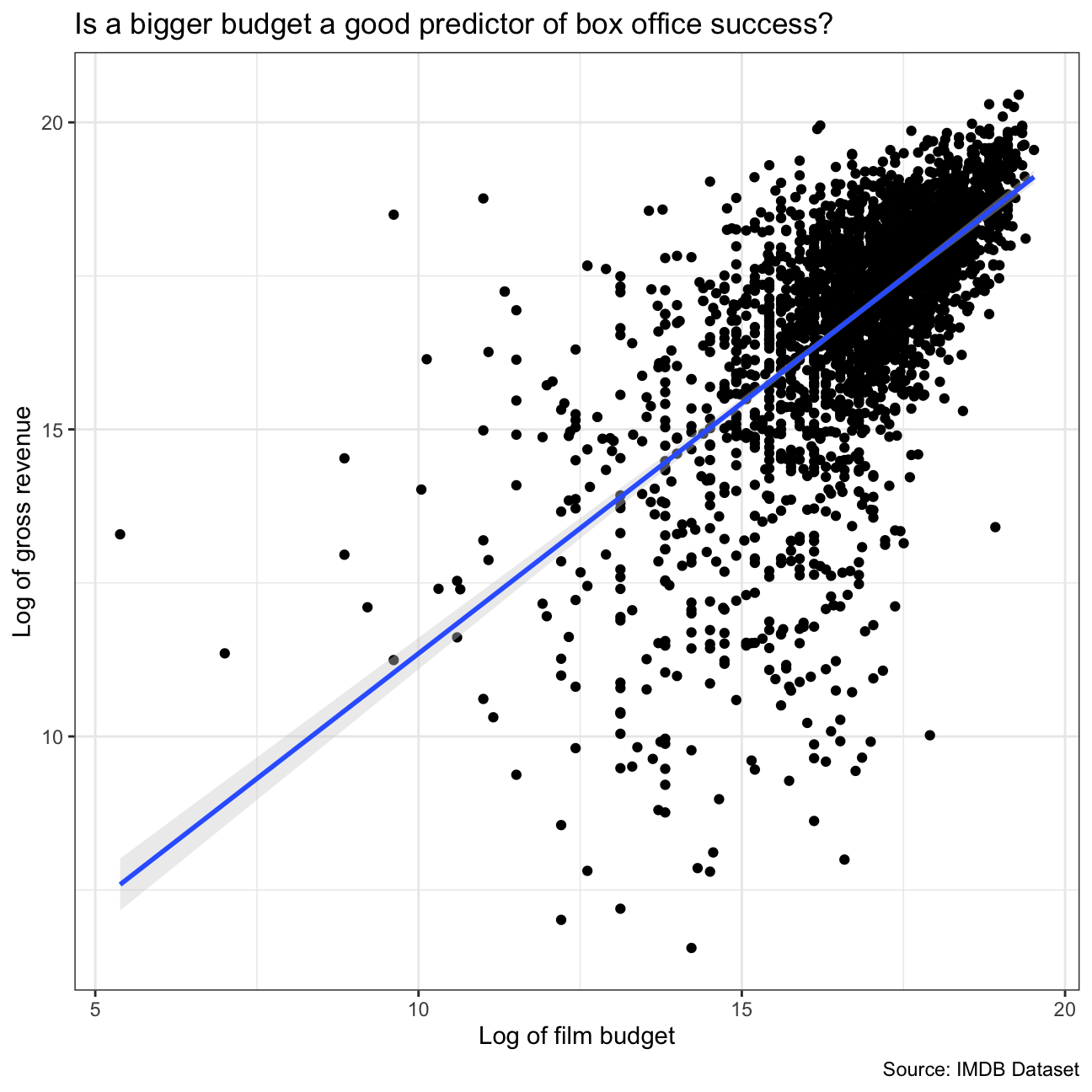
How do IMDB ratings correlate with box office perfromance across different movie genres?
From these plots it seems that IMDB rating is not a good indicator of a movie’s box office revenue because for most movie genres most movies incline to the same revenue level regardless of their IMDB ratings. It is strange in the dataset that for some genres of movies not much data available.
ggplot(movies, aes(x=rating, y=gross))+
geom_point()+
facet_wrap(~genre, nrow = 6)+
labs(title="IMDB Ratings as a predictor of box office performance",
x ="IMDB Ratings",
y ="Gross",
caption = "Source: IMDB dataset")+
theme_bw()+
expand_limits(y=0, x = 0)+
NULL
IMDB ratings: Differences between directors
Now we would like to explore whether the mean IMDB rating for Steven Spielberg and Tim Burton are the same or not. ## Produce the data we will use
Burton_Spielberg <- movies %>%
filter(director %in% c("Steven Spielberg", "Tim Burton"))Below is the calculated the confidence intervals for the mean ratings of these two directors and as you can see they overlap. We will reproduce this graph and run a hpothesis test using both the t.test command and the infer package to simulate from a null distribution, where we assume zero difference between the two.
Confidence intervals for the mean ratings of Steven Spielberg and Tim Burton
g1 <- Burton_Spielberg %>%
group_by(director) %>%
summarize(n = n(),
mean_rating = mean(rating, na.rm = TRUE),
SD_directors = sd(rating, na.rm = TRUE),
SE_directors = SD_directors/sqrt(n),
t_critical = qt(0.975, n-1),
lower95_ci = mean_rating - t_critical*SE_directors,
upper95_ci = mean_rating + t_critical*SE_directors)
g1 %>%
ggplot(mapping = aes(x = mean_rating, y= reorder(director, mean_rating)))+
geom_point(aes(color = as.factor(director)), show.legend = FALSE, size = 5) +
geom_errorbar(aes(xmin = lower95_ci, xmax = upper95_ci, color = as.factor(director)), width = 0.1, show.legend = FALSE, size = 1.8) +
geom_rect(aes(xmin = max(lower95_ci), xmax = min(upper95_ci), ymin = -Inf, ymax = Inf), alpha = 0.1, fill = "black") +
theme_minimal()+
labs(x = "Mean IMDB Rating",
y = "",
title = "Do Spielberg and Burton have the same mean IMDB rating?",
subtitle = "95% confidence intervals overlap"
)+
geom_text(aes(label = round(mean_rating,2)), vjust=-1, size=6)+
geom_text(aes(x=upper95_ci, label = round(upper95_ci,2)), vjust=-1, size=5)+
geom_text(aes(x=lower95_ci, label = round(lower95_ci,2)), vjust=-1, size=5)+
NULL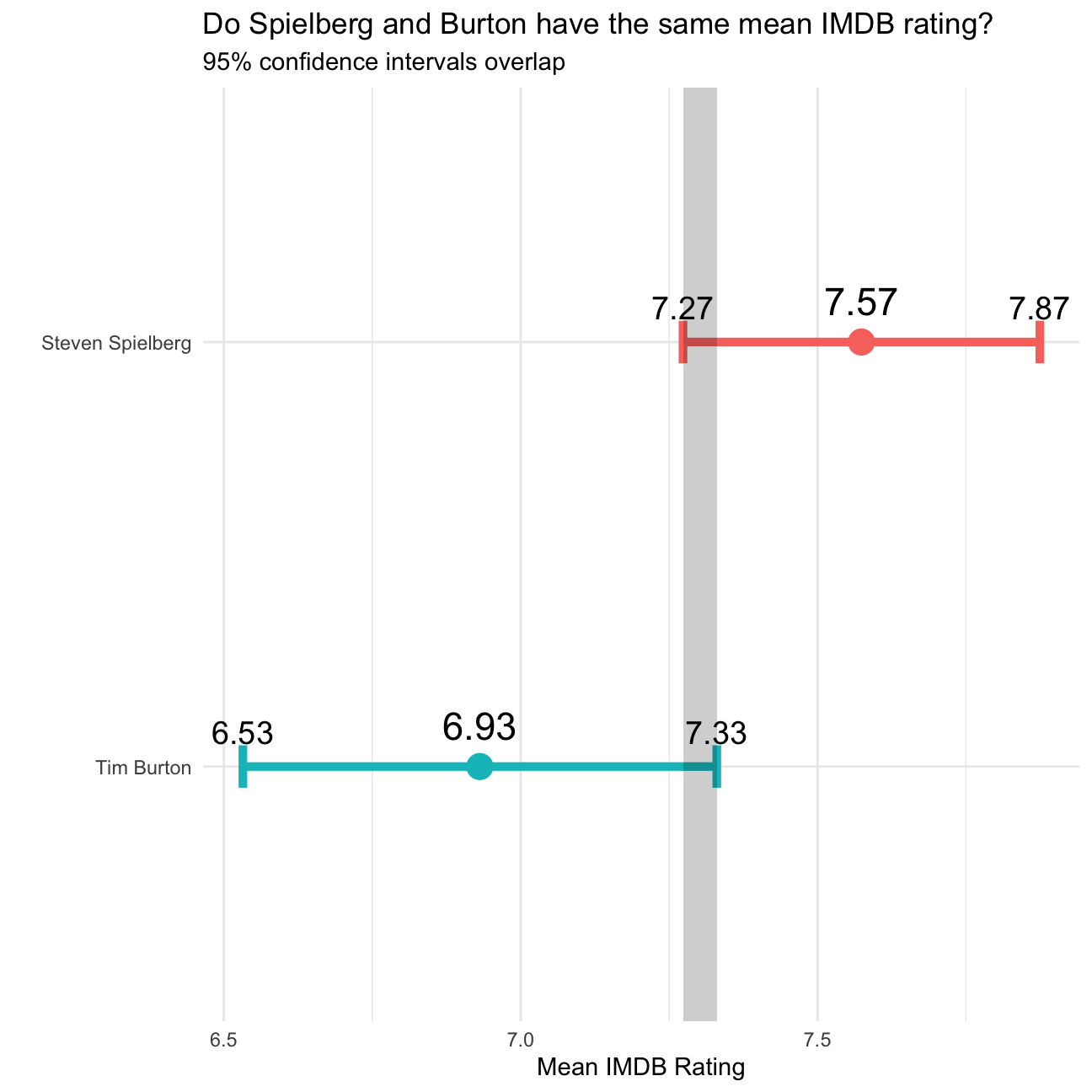
Hypothesis test with formula
- Null hypotheses: The mean IMDB rating for Steven Spielberg and Tim Burton are the same
- Alternative hypotheses: The mean IMDB rating for Steven Spielberg and Tim Burton are different
- p-value: if p-value is lower than 5%, then reject H0 and think the mean IMDB rating for Steven Spielberg and Tim Burton are different
t.test(rating ~ director, data = Burton_Spielberg)##
## Welch Two Sample t-test
##
## data: rating by director
## t = 3, df = 31, p-value = 0.01
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.16 1.13
## sample estimates:
## mean in group Steven Spielberg mean in group Tim Burton
## 7.57 6.93Hypothesis test with infer
- Null hypotheses: The mean IMDB rating for Steven Spielberg and Tim Burton are the same
- Alternative hypotheses: The mean IMDB rating for Steven Spielberg and Tim Burton are different
- p-value: if p-value is lower than 5%, then reject H0 and think the mean IMDB rating for Steven Spielberg and Tim Burton are different
# initialize the test, which we save as `directors_diff`
directors_diff <- Burton_Spielberg %>%
specify(rating ~ director) %>%
# the statistic we are searching for is the difference in means, with the order being "Steven Spielberg", "Tim Burton"
calculate(stat = "diff in means", order = c("Steven Spielberg", "Tim Burton"))
# simulate the test on the null distribution, which we save as null
directors_null_dist <- Burton_Spielberg %>%
specify(rating ~ director) %>%
hypothesize(null = "independence") %>%
generate(reps = 1000, type = "permute") %>%
calculate(stat = "diff in means", order = c("Steven Spielberg", "Tim Burton"))
# Visualising to see how many of these null permutations have a difference
directors_null_dist %>% visualize() +
shade_p_value(obs_stat = directors_diff, direction = "two-sided")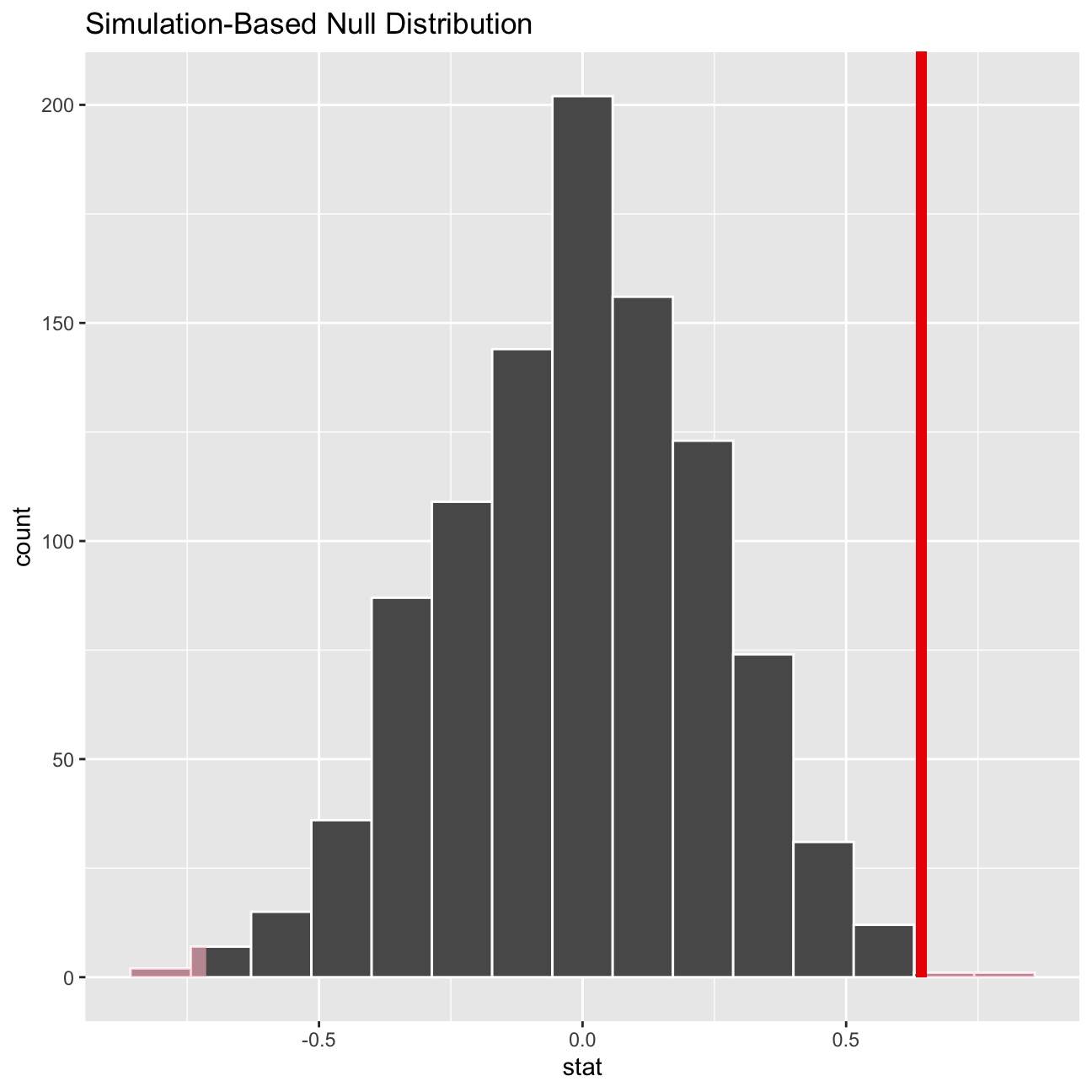
# Calculating the p-value for the hypothesis test
directors_null_dist %>%
get_p_value(obs_stat = directors_diff, direction = "two_sided")## # A tibble: 1 x 1
## p_value
## <dbl>
## 1 0.004From the hypothesis test, we can see that the t-stat is 3 and the p-value is 1% which is smaller than 5%, so we reject the null hypothesis and conclude that the the difference in mean IMDB ratings for Steven Spielberg and Tim Burton is statistically significant, specifically the mean rating of Steven Spielberg is higher. This is just like what we expected, as we all prefer Steven Spielberg.